LOS CUADRILATEROS
COMCEPTO:
Son pilogonos de cuatro lados donde se pueden trazar un maximo dos diagonales .
CLASIFICACION DE LOS CUADRILATEROS:
paralogramo
-cuadrado
Los cuadriláteros se clasifican en:
- Paralelogramos (sus lados enfrentados son paralelos)
- Rectángulos
- Oblicuángulos
- Trapecios (dos de sus lados son paralelos y los otros dos no)
- Trapecio rectángulo
- Trapecio isósceles
- Trapecio escaleno
- Trapezoide (no tiene lados paralelos)
- Trapezoide simétrico o deltoide
- Trapezoide asimétrico
Fórmulas
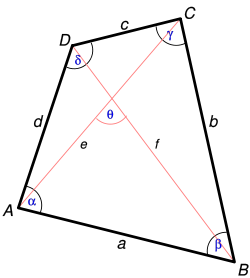
Los cuatro lados de un cuadrilátero (a, b, c, d),
los cuatro vértices (A, B, C, D) y sus dos diagonales (e, f).
los cuatro vértices (A, B, C, D) y sus dos diagonales (e, f).
- La suma de los ángulos internos es igual a 360° (grados sexagesimal) o 2π radianes. La suma de los ángulos exteriores en todo polígono regular es igual a 360°.
- El área de un cuadrilátero puede determinarse de diferentes formas:







No hay comentarios:
Publicar un comentario